
许多同学们在备考MAP数学考试的时候,会遇上需要计算几何体体积的问题。今天由教研团队的Lumi老师将带大家从深层面理解什么是体积,该如何计算体积以及体积计算的底面逻辑做一个的拆解。
MAP数学
测试概况:
年级:K-12年级
时间:约60分钟
题目:约52题
题型:选择题、拖拽匹配题等
测试内容:
Number and Operations
数与计算
Algebra
代数
Geometry
几何
Statistics and probability
统计与概率
Problem-solving, reasoning, and proofs
问题解决,论证与证明
事实上,MAP数学的备考和国内的知识体系非常相似,但又并不完全覆盖;熟知北师大教材的同学们一定理解体积的计算在深圳的北师大教材体系下是小学就已经接触的知识点了;但是在MAP数学中,他的考试横跨了多个年级段。
MAP的考试中基本上全部都是选择题,所以同学们如果在遇到体积类的计算问题,却想不起公式,是没有办法和代数(Algebra)的多数题目一样,直接代入去找寻答案的。因此老师整理了一下MAP考试中我们有可能遇到的体积问题类型如下:

MAP阅读考试的这些考法和国内K12体系下的考试是非常不一样的,甚至于教研团队的老师们在给一些学生上课的时候,学生会出现压根看不懂题目的情况。
那么如何理解体积的定义呢?
The volume of a 3D figure refers to the number cubic units needed to fill the figure. Or, put it more simple, “How much will fit in here?” The answer is volume.
看了那么多,是不是有点晕头转向的?没问题,Lumi老师给您总结一下,体积就是:
1. 这个物体占空间多大;
2. 这个物体需要多少立方单位的水可以填满?
需要填满的水越多,说明他的体积越大。那么在这里需要各位注意一下,所谓体积的单位一般情况下都是带立方的,原文是那么描写的:Volume is measured in cubic units.
有同学会感到迷惑,升(L)和毫升(mL)并不带立方,为什么是体积单位呢?原因是:这里我们提到的立方是指概念上立方,不是文字上立方,升和毫升是容积单位。
那么接下来我们来理解一下体积的由来,其实任何在我们生活中能看到的物体都是有厚度的,哪怕是一张纸也是有厚度的。许多孩子从一开始认识体积的时候就会开始接触到这个概念:假如一张纸没有厚度,那么很多张纸叠起来同样不会有厚度。因此在一张纸的基础上,我们知道如何计算他的面积时,就有了最基础的体积公式:

也就是说,所有的规则类的棱柱或者圆柱我们都可以通过这样的公式来计算它的体积,唯一不同的只是他的底(Base)有什么区别罢了。
那么如果底是:
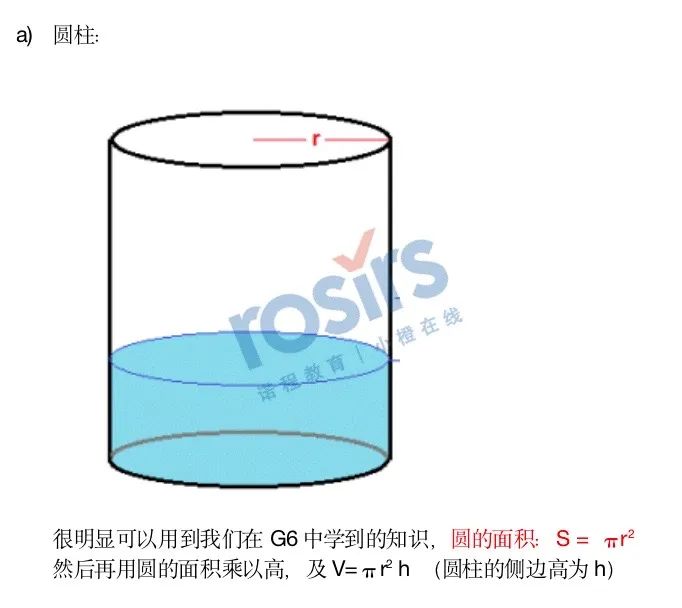
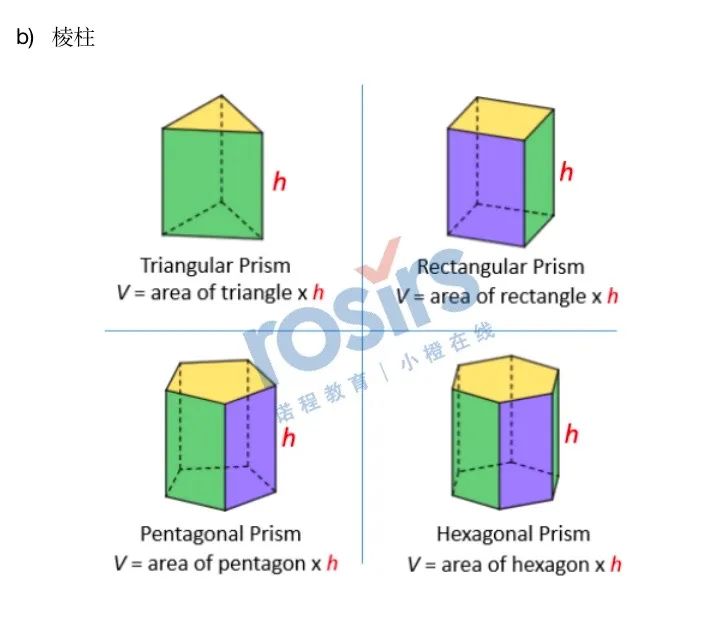

真题题目1:

正确答案:D
解析:

真题题目2:
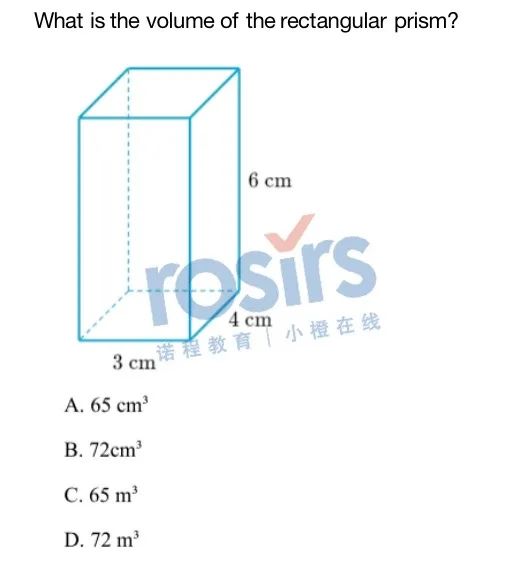
正确答案:B
解析:

*版权声明:本文所有文字均为原创,未经允许,不得私自盗用或转载。

